Statistic NLP 를 앞으로 다룹니다. 이는 통계를 기반으로 하는 NLP : Frequentist Approach (빈도를 활용), Bayesian Approach (베이지안 활용) 방법이 있습니다.


확률 기반의 자연어 분석기법

Binary Distribution (이항분포) 를 계산하는 방법으로 Berboulli Distribution (베르누이 분포) 공식을 활용 합니다.

확률의 계산

확률값을 계산하는 경우

P(H) = 셉타
P(T) = 1 - 셉타 (P>=0)
P(HHTHT) = 셉타 * 셉타 * (1-셉타) * 셉타 * (1-셉타)
         = 셉타 ^3 * (1- 셉타)^2

D = 앞,앞,뒤,앞,뒤
n = 5
p = 셉타
a = 확률
P(D|셉터) = 셉타^(aH) (1-셉타)^((n-a)H)

MLE (Maximum Likelihood Estimation)

셉타^ : Best Candidate

$$셉타^ = argmax P(D 셉타)$$ # 원래의 셉타 와 셉타^ 이 유사하도록 모델을 만든다

미분을 사용하여 개별 theta 값을 활용하여 미분을 합니다

PCA Learning

Probably Approximate Correct (허용 가능한 오류율 범위내 모델을 생성)

셉타^ 은 관찰데이터를 활용하여 최대추정가능 확률을 계산한 것

실제로 존재할 셉타* 값과 비교하여 관찰횟수가 적으면 셉타^ 은 (오류율 > 0) 이 발생 합니다.

Error Bound : P( 셉타^ - 셉타* >= 오류율) <= 2e ^(-2Ne^2)

오류율을 줄이기 위해서는 N (반복횟수) 를 키우면 된다.

MAP (Maximum A Posterior Estimation)

베이즈 정리를 바탕으로 MLE 와 MLP

MLE 는 관찰결과를 바탕으로 결과를 도출한 결과인 만큼, Posteriori(사전지식들) 를 활용하여 측정된 모델을 보정해 주는 방식이 도출하게 됩니다.

Bayes Theorem

베이지안 모델을 활용하면 확률의 순서를 바꿔서 적용할 수 있습니다.

경험확률값이 없어도 CDF 모델에서 확률값을 만들어서 계산을 할 수 있다.

Logistic Regression

Linear Regression 의 활용

f^ 측정한 확률값을 활용하여, 모델의 결과값을 추정

\[h:f^(x;셉터) = Sigma ^n _(i=0)\]

Squared Error (Sum/ Meam Squared Error 를 최소로 하는 함수를 활용하여 회귀 모델을 추정합니다.)

Optimal Classification and Bayer Risk

비선형이 정확도는 높일 수 있지만 Dicision Binary 를 경게로 차이를 오히려 더 벌릴 수 있는 한계도 함께 존재한다.

Bayse Risk : 잠재적인 위험도를 측적해야 한다

Logistic Regression Classifire

Sigmoid Function

-1~1 사이의 값으로 확률 함수와는 무관하게 활용되고, weight 를 변경 할 것인지/ 아닌지 를 판단하는 활성화 여부 판단함수 로 주로 활용 됩니다.

참고로 weight 값은 역전파를 활용한 BackPropagate 편미분을 활용하여 전체적인 weight 값이 훈련 과정마다 보정 됩니다.

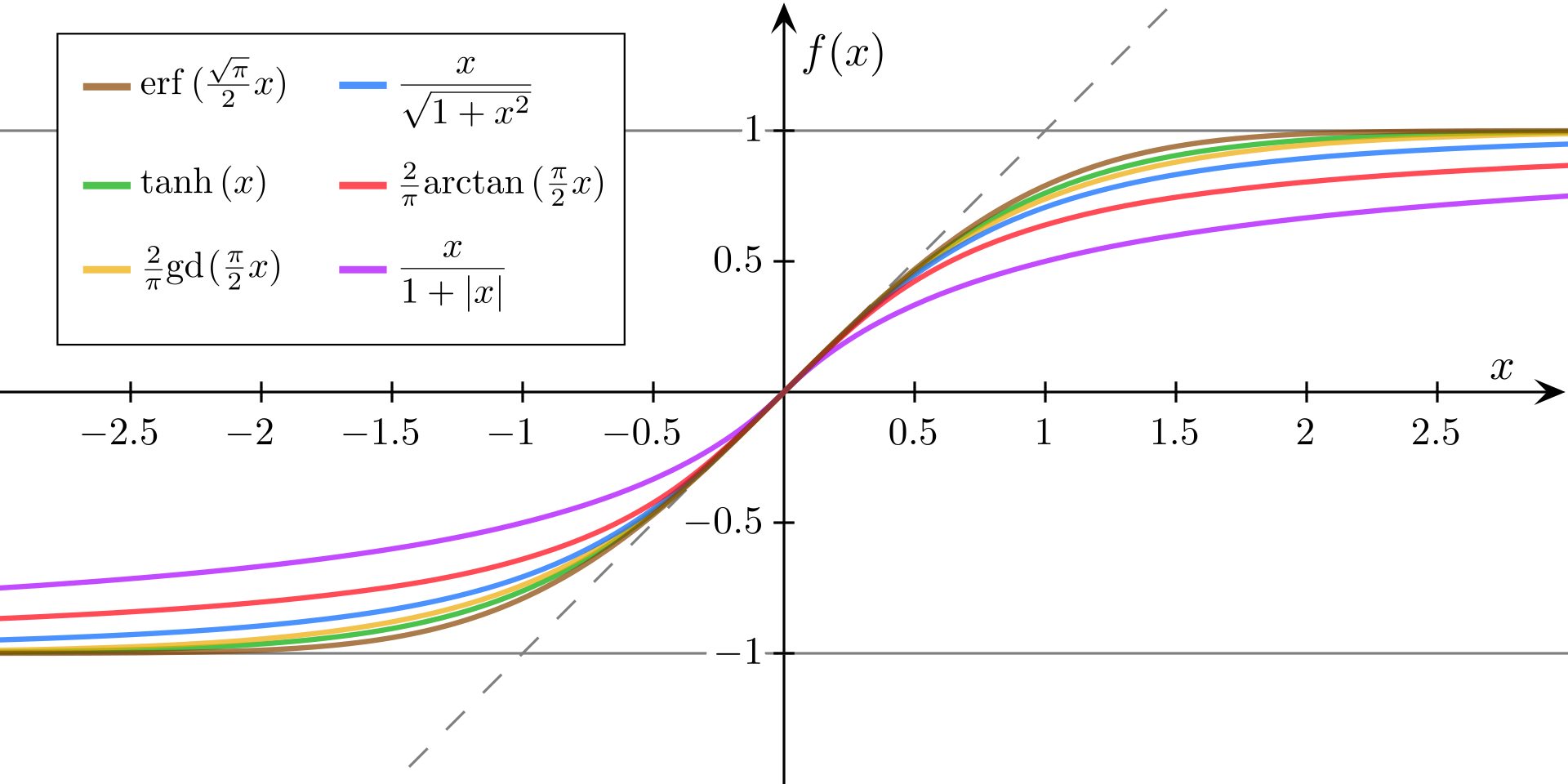
Logistic Function

\[f(x) = 1 / 1 + e^(-x)\]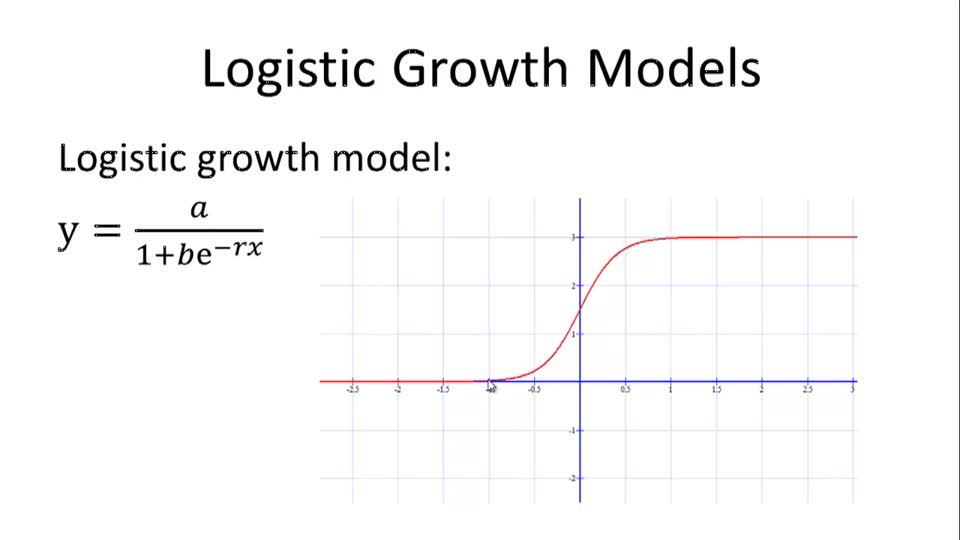

Logistic Regression

베르누이 분포 확률을 활용하여 확률값을 활용하여 회귀모델을 도출 합니다

Maximum Conditional Likelihood Estimation (MCLE)

Gradient Descent

Taylor Expansion 의 공식을 활용하여 BackPropaget 을 도출 합니다

RosenBrock Function

3차원 공간에서 최적의 점을 찾는다


Supervised Learning

Super Vised

SuperVised

  1. 분류모델 (불연속모델) 손글씨 인식, 약분류
  2. 회귀모델 (연속모델) Object Detection, Linear/ Logistic Regression (값을 찾는 모델링)

unSuperVised

  1. 클러스터링 (불연속모델) K-means, Mean-shift, GMM(가오시안믹스드 모델), LDA,
  2. 차원의 축소(연속모델) PCA, LDA (KERNEL)

Naive Bayse Classifier

https://images.slideplayer.com/39/10998954/slides/slide_11.jpg

MLE : argmax() 값을 찾음 MLP : 사전지식을 활용하여 모델을 추정

argmin : 오차가 작은 값을 찾는다 argmax : 최대 성능을 갖는 값을 찾는다

\(argmin_{f}P (f(x) =/= Y) = f^*\) (옵티멀한 분류기) \(argmax_(y=x)P(Y=y|X=x) = f^*(x)\) (Naive Bayse 모델링)

MLE & MAP

\[argmax_{theta}P(D|theta)\]

MLE 는 Likelihood 를 활용하여 데이터가 많으면 성능이 좋지만, MAP 는 **데이터가 적어도 (특정 확률분포 데이터) 효과적인 모델을 추정할 수 있어서 모델링에 폭넓게 활용 가능합니다.

Example

https://www.saedsayad.com/images/naive_bayes_example_2.png

Positive/ Negative Sampling 방법으로 Machine Learning 이전에 분류 방식으로 Naive Bayse 기법을 활용하였고, 현재에도 Pre Processing 과정에서 위 내용을 활용하고 있습니다.

Assumption, Conditional Independence

Conditional Independence : Naive Bayse 모델링 구현시 Token 간은 모두 독립으로 가정하면, 개별 단어token 의 확률 곱으로도 전체적인 모델의 확률을 구현할 수 있다

물론 Token 간의

P(스팸 관련token, token, token..) = P(token, token 스팸)P(스팸)
\[\nabla_\boldsymbol{x} J(\boldsymbol{x})\]

Conditional vs Marginal

  1. Conditional Indepandent : 조건이 주어질 때, 조건부 확률에 영향이 없을 때
  2. Marginal Independence : 상대방의 행동이 자신에게도 영향을 준다 P(a b) = P(a)

Naive Bayse Classifier

문제점으로는

  1. Naive Assumption (상관성이 높은 단어들의 처리가 어렵다) = > 우선은 넘어가자
  2. Probability Estimations (MLE 는 데이터가 부족하면 불충족, MAP 는 애매한 모델이 생성)

Question!!

셉타^ : 조건부 확률의 최대값 (몇번쨰 셉타값) 확률값인가? 아님 횟수값인가? aH, aT : 관찰확률 Sigmoid 가 확률과 무관한 이유는?

Q. Sigmoid 함수를 활용하여 모델을 예측하는게 좋은 이유는 Taylor 급수처럼 최적화가 유용해서 인가? Q. “대출” 키워드 문서가 스팸일 확률의 계산을 어떻게 바꿨다고? Q. conditional Independence 관계에서 개별 독립을 전제시 Token 갯수를 어떻게 줄이나?